TRIGONOMETRI

Persamaan trigonometri berbentuk $a\cos x+b\sin x=c$ untuk bilangan real tak nol $a,b,c$ dapat diselesaikan dengan syarat $a^2+b^2\ge c^2$. Bentuk tersebut ekuivalen dengan $k\cos (x-p)$ dengan keterangan sebagai berikut.
$$\begin{array}{cc}k& =\sqrt{a^2+b^2}\\ \tan p& =\frac{b}{a},-\pi \le x\le \pi \end{array}$$Selain itu, bisa juga dituliskan dalam bentuk $k\sin (x+p)$ dengan keterangan sebagai berikut.
$$\begin{array}{cc}k& =\sqrt{a^2+b^2}\\ \tan p& =\frac{a}{b},-\pi \le x\le \pi \end{array}$$Perbedaannya hanya pada bentuk perbandingan tangennya. Perhatikan juga bahwa besar sudut $p$ yang akan diambil tergantung dari tanda kepositivan koefisien $\cos x$ dan $\sin x$ mengikuti tabel berikut.
$$\begin{array}{ccc}\text{Koef.}\cos x& \text{Koef.}\sin x& \text{Kuad}\text{ran}p\\ +& +& \text{I}\\ –& +& \text{II}\\ –& –& \text{III}\\ +& –& \text{IV}\end{array}$$Bukti:
Ekspansi dari bentuk $k\cos (x-p)$ dengan menggunakan identitas selisih sudut adalah sebagai berikut.
$$\begin{array}{cc}k\cos (x-p)& =k(\cos x\cos p+\sin x\sin p)\\ & =\left(k\cos p\right)\cos x+\left(k\sin p\right)\sin x\end{array}$$Misal
$$\{\begin{array}{c}a=k\cos p\\ b=k\sin p\end{array}$$Kedua persamaan dibandingkan dan kita peroleh
$$\begin{array}{cc}\frac{k\sin p}{k\cos p}& =\frac{b}{a}\\ \tan p& =\frac{b}{a}\end{array}$$Kedua persamaan dikuadratkan, lalu dijumlahkan, dan kita peroleh
$$\begin{array}{cc}\left(k^2{\cos }^{2}p\right)+\left(k^2{\sin }^{2}p\right)& =a^2+b^2\\ k^2({\cos }^{2}p+{\sin }^{2}p)& =a^2+b^2\\ k^2\left(1\right)& =a^2+b^2\\ k& =\sqrt{a^2+b^2}\end{array}$$

Ekspansi dari bentuk $k\sin (x+p)$ dengan menggunakan identitas selisih sudut adalah sebagai berikut.
$$\begin{array}{cc}k\sin (x+p)& =k(\sin x\cos p+\cos x\sin p)\\ & =\left(k\cos p\right)\sin x+\left(k\sin p\right)\cos x\end{array}$$Misal
$$\{\begin{array}{c}a=k\sin p\\ b=k\cos p\end{array}$$Kedua persamaan dibandingkan dan kita peroleh
$$\begin{array}{cc}\frac{k\sin p}{k\cos p}& =\frac{a}{b}\\ \tan p& =\frac{a}{b}\end{array}$$Kedua persamaan dikuadratkan, lalu dijumlahkan, dan kita peroleh
$$\begin{array}{cc}\left(k^2{\cos }^{2}p\right)+\left(k^2{\sin }^{2}p\right)& =a^2+b^2\\ k^2({\cos }^{2}p+{\sin }^{2}p)& =a^2+b^2\\ k^2\left(1\right)& =a^2+b^2\\ k& =\sqrt{a^2+b^2}\end{array}$$(Terbukti)

Soal Nomor 1
Besar sudut yang sesuai dengan gambar di bawah adalah $\cdots \cdot$

A. ${30}^{\circ }$                 C. ${300}^{\circ }$                     E. ${390}^{\circ }$            
B. ${60}^{\circ }$                 D. ${330}^{\circ }$                          

Soal Nomor 2
Besar sudut $\frac{3}{4}\pi \text{rad}$ sama dengan $\cdots \cdot$
A. ${75}^{\circ }$                   C. ${135}^{\circ }$               E. ${270}^{\circ }$             
B. ${105}^{\circ }$                 D. ${210}^{\circ }$                   

Soal Nomor 3
Besar sudut ${72}^{\circ }$ sama dengan $\cdots \text{rad}$
A. $\frac{1}{5}\pi$                   C. $\frac{2}{3}\pi$                  E. $\frac{5}{6}\pi$               
B. $\frac{2}{5}\pi$                   D. $\frac{3}{4}\pi$                               

Soal Nomor 4
Perhatikan gambar di bawah.

Segitiga $ABC$ siku-siku di $C$. Pernyataan berikut ini benar, kecuali $\cdots \cdot$
A. $\sin \alpha =\frac{BC}{AB}$                D. $\cos \beta =\frac{BC}{AC}$
B. $\sin \beta =\frac{AC}{AB}$                 E. $\tan \alpha =\frac{BC}{AC}$
C. $\cos \alpha =\frac{AC}{AB}$

Soal Nomor 5
Perhatikan gambar berikut!

Nilai $\cos \alpha$ adalah $\cdots \cdot$
A. 1                         C. $\frac{1}{2}\sqrt{3}$                  E. $\frac{1}{3}\sqrt{3}$
B. $\sqrt{3}$                     D. $\frac{1}{2}$      

Soal Nomor 6
Diketahui koordinat titik $A(-2\sqrt{2},-2\sqrt{2})$. Koordinat kutub dari titik $A$ adalah $\cdots \cdot$
A. $(4,{210}^{\circ })$                 D. $(5,{240}^{\circ })$ 
B. $(2,{240}^{\circ })$                 E. $(4,{225}^{\circ })$
C. $(2,{225}^{\circ })$

Soal Nomor 7
Segitiga $KLM$ memiliki koordinat $K(-5,-2),L(3,-2)$, dan $M(-5,4)$. Nilai $\cos L$ dan $\tan M$ berturut-turut adalah $\cdots \cdot$
A. $\frac{3}{5}$ dan $\frac{3}{4}$              D. $\frac{4}{5}$ dan $\frac{3}{4}$
B. $\frac{3}{4}$ dan $\frac{3}{5}$              E. $\frac{4}{5}$ dan $\frac{4}{3}$
C. $\frac{3}{4}$ dan $\frac{4}{3}$

Soal Nomor 8
Diketahui segitiga $PQR$ memiliki koordinat $P(-3,2),Q(-3,-2)$, dan $R(3,2)$. Nilai $\frac{3\sec R}{\csc Q}=\cdots \cdot$
A. $1$                  C. $3$                      E. $2\sqrt{13}$
B. $2$                  D. $\sqrt{13}$         

Soal Nomor 9
Diketahui $△ABC$ siku-siku di $B$. Jika $\cos A=\frac{3}{4}$, nilai $\cot A=\cdots \cdot$
A. $\sqrt{7}$                                 D. $\frac{3}{4}\sqrt{7}$
B. $\frac{3}{7}\sqrt{7}$                             E. $\frac{4}{3}\sqrt{7}$
C. $\frac{4}{7}\sqrt{7}$

Soal Nomor 10
Diketahui $P$ sudut lancip. Jika $\tan P=\frac{5\sqrt{11}}{11}$, maka nilai $\sin P=\cdots \cdot$
A. $\frac{5}{\sqrt{11}}$                               D. $\frac{\sqrt{11}}{5}$
B. $\frac{6}{\sqrt{11}}$                               E. $\frac{\sqrt{11}}{6}$
C. $\frac{5}{6}$

Soal Nomor 11
Diketahui $△ABC$ siku-siku di $C$. Jika $\sin B=p$, maka nilai $\tan B=\cdots \cdot$
A. $\frac{p}{\sqrt{1-p^2}}$                              D. $\frac{p}{\sqrt{p^2-1}}$
B. $\frac{1}{\sqrt{1-p^2}}$                              E. $\frac{\sqrt{1-p^2}}{p}$
C. $\frac{1}{\sqrt{p^2-1}}$

Soal Nomor 12
Perhatikan $△KLM$ di ba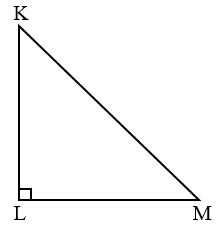wah!

Jika $\cos K=\frac{1}{a}$, maka nilai $\sin K\tan K=\cdots \cdot$
A. $\frac{a^2+1}{a}$                             D. $\frac{a}{a^2+1}$
B. $\frac{a^2-1}{a}$                              E. $\frac{a^2-1}{a^2+1}$
C. $\frac{a}{a^2-1}$

Soal Nomor 13
Berdasarkan gambar di bawah, jika $\cos \theta =\frac{2}{3}$, nilai $x$ yang memenuhi adalah $\cdots \cdot$

A. $3\sqrt{5}$                                 D. $6\sqrt{5}$
B. $4\sqrt{5}$                                 E. $7\sqrt{5}$
C. $5\sqrt{5}$

Soal Nomor 14
Jika $\tan \alpha =\frac{1}{a}$ dengan $0^{\circ }<\alpha <{90}^{\circ }$, maka nilai dari $\cos \alpha -\frac{1}{\sin \alpha }$ sama dengan $\cdots \cdot$
A. $\frac{a^2+a+1}{\sqrt{1+a^2}}$                       D. $\frac{a^2-a-1}{\sqrt{1+a^2}}$
B. $\frac{a^2+a-1}{\sqrt{1+a^2}}$                        E. $\frac{-a^2+a-1}{\sqrt{1+a^2}}$
C. $\frac{a^2-a+1}{\sqrt{1+a^2}}$

Soal Nomor 15
Segitiga $KLM$ siku-siku di $L$. Jika $\sin M=\frac{2}{3}$ dan $KL=\sqrt{20}\text{cm}$, maka panjang sisi $KM=\cdots \text{cm}$.
A. $2\sqrt{5}$                                 D. $3\sqrt{10}$
B. $3\sqrt{5}$                                 E. $4\sqrt{10}$
C. $2\sqrt{10}$

Soal Nomor 16
Segitiga $DEF$ memiliki sisi tinggi $DF$. Jika luas segitiga tersebut $9{\text{cm}}^2$ dan panjang $EF=3\text{cm}$, maka nilai $\cos E=\cdots \cdot$
A. $\frac{1}{5}\sqrt{5}$                               D. $\frac{4}{5}\sqrt{5}$
B. $\frac{2}{5}\sqrt{5}$                               E. $\sqrt{5}$
C. $\frac{3}{5}\sqrt{5}$

Soal Nomor 17
Sesuai dengan gambar di bawah, nilai perbandingan ${\sin }^2\theta$ adalah $\cdots \cdot$

A. $\frac{a^2-d^2}{f^2+g^2}$                          D. $\frac{a^2+b^2}{f^2-g^2}$
B. $\frac{a^2+b^2}{f^2+g^2}$                          E. $\frac{a^2-b^2}{f^2+g^2}$
C. $\frac{a^2-b^2}{f^2-g^2}$

Soal Nomor 18
Jika $\tan x=-\frac{2}{3}$, maka nilai dari $\frac{5\sin x+6\cos x}{2\cos x-3\sin x}$ adalah $\cdots \cdot$
A. $-\frac{7}{6}$                     C. $\frac{1}{3}$                     E. $\frac{7}{6}$
B. $-\frac{2}{3}$                     D. $\frac{2}{3}$            

Soal Nomor 19
Dalam segitiga siku-siku $ABC$ di bawah, panjang $BC=a$ dan besar $\angle ABC=\beta$. Panjang garis tinggi 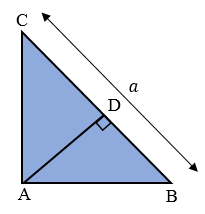$AD=\cdots \cdot$

A. ${\sin }^2\beta \cos \beta$              D. $a\sin \beta {\cos }^2\beta$
B. $a\sin \beta \cos \beta$             E. $a\sin \beta$
C. $a{\sin }^2\beta$

Soal Nomor 20
Perhatikan gambar di bawah!

Segi empat $ABCD$ siku-siku di $A$ dan $C$. Diketahui besar $\angle ABD=\alpha ,\angle CBD=\beta$, dan panjang $AD=p$. Panjang sisi $BC$ adalah $\cdots \cdot$
A. $p\sin \alpha \cos \beta$                      D. $\frac{p\cos \beta }{\sin \alpha }$
B. $p\cos \alpha \sin \beta$                      E. $\frac{p\sin \beta }{\sin \alpha }$
C. $\frac{p\sin \alpha }{\cos \beta }$

Bagian Uraian

Soal Nomor 1
Tentukan nilai $\sin \alpha$, $\cos \alpha$, $\tan \alpha$, $\sec \alpha$, $\csc \alpha$, dan $\tan \alpha$ pada segitiga berikut.

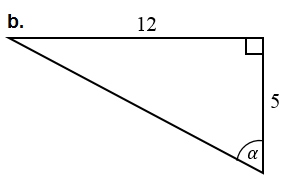
c.

Soal Nomor 2
Segitiga $KLM$ siku-siku di $K$. Jika nilai $\sin L=0,28$, tentukan:
a. $\tan L$                      b. $\tan M$

Soal Nomor 3
Perhatikan segitiga siku-siku berikut!

Buktikan pernyataan berikut!
a. ${\sin }^{2}C+{\cos }^{2}C=1$
b. ${\csc }^{2}A-{\cot }^{2}A=1$

Soal Nomor 4
Perhatikan gambar berikut!

Jika panjang $AD=1\text{cm}$, tunjukkan bahwa panjang $BD=\frac{\tan \alpha }{\tan \beta -\tan \alpha }\text{cm}.$

Soal Nomor 5
Diketahui persegi $ABCD$ mempunyai panjang sisi $6a$ satuan. Kedua diagonalnya berpotongan di titik $O$. Jika titik $P$ terletak pada diagonal $AC$ dengan perbandingan $OP:PC=1:2$, tentukan nilai $\sin \angle PBO$.

Soal Nomor 6 ($★$ HOTS $★$)
Gambar berikut adalah lingkaran satuan dan segitiga yang berpotongan. Ruas garis yang dipertebal membentuk bangun datar trapesium siku-siku. Tentukan luas trapesium tersebut.

Soal Nomor 7 ($★$ HOTS $★$)
Seseorang berada pada ketinggian $h$ di atas permukaan air suatu danau. Terlihat di atasnya seekor burung pada sudut elevasi $\alpha$ dan bayangannya dalam air pada sudut depresi $\beta$, seperti tampak pada gambar berikut.

Berapa ketinggian terbang burung tersebut?